|
 |
 |
Volume
6 - Issue 11
NOVEMBER - 2008 |
By Prof. G. Venkataraman
Loving Sai Ram and greetings from Prashanti Nilayam. I hope I have not lost you after I made the change of gear that took you from the Cosmos to Basic Physics. Just to remind you, I first offered a lightning glimpse of Physics as it evolved under Newton and later physicists [almost every one of them from Europe], till the end of the nineteenth Century. The highpoint of this period was Maxwell’s great Electromagnetic Theory of Radiation, into which all phenomena of optics could be neatly fitted. Indeed, Maxwell’s theory led to incredible practical benefits that are being conferred upon us right to this day; take anything from cell phones to microwave ovens, and we have to thank Maxwell for all of them. You might say: “OK, but what has all that got to do with our Quest for Infinity?” I am coming to that but would have to do it in stages, for now the ball game gets rather subtle; and we have first to go through the rather mysterious subject called Quantum Mechanics. Right now, I am trying to set the stage for describing its birth! Hope all that reassures you that I have really not lost my way! 19 th Century Scientists Struggle with some Imponderables
Before I get to what I want to say this time, let us remember that Niels Bohr [see QFI 18] wanted to have a theory for why atoms were emitting the characteristic line spectra. To Bohr, it all seemed as if each atomic species was singing its own song, and he wanted to know why they were singing “songs” [read emitting spectra] in the first place, and why these songs [read spectra] were different from each other. I told you that Bohr came up with a model based on the idea that an atom was really like a mini solar system with a tiny, tiny nucleus at the centre [that played the role of the sun] while the electrons moved around like planets, revolving around the nucleus in various orbits. Bohr tried to apply this idea to the hydrogen atom because it was the simplest among the atoms with only one electron going round the nucleus, which, by the way, was nothing more than a single proton. The model was utterly simple but the result that Bohr got was disastrous. Bohr applied Classical Mechanics, which was all that one had at that time. And when Bohr went through his calculation, he found to his horror that the atom hardly lived, in fact less than a second. Imagine that! Here we are in a Universe that is billions of years old with hydrogen atoms all over the place. We have them here on planet Earth too. In fact, chemistry students are taught how to make gaseous hydrogen with what is called the Kipp’s apparatus. But Bohr’s theory said that the hydrogen atom had no business to exist! The electron must rapidly spiral into the proton, wiping out the hydrogen atom! Bohr knew that there was something wrong, and very correctly he suspected that the problem lay in the Classical Mechanics that he had applied to the hydrogen atom. This is what I am trying to slowly draw your attention to. You see, even as the nineteenth century was drawing to a close and physicists were exuberantly celebrating the great triumphs scored during the nineteenth century, they were also getting signals that all was not quite OK with Classical Physics. The signals came from different directions, and often they did not seem connected. For example, there was Planck who found that a classical formula could not explain the spectrum of Blackbody Radiation [see QFI 19]. Then there was the photo-electric effect that defied explanation within the framework of Classical Physics. Meanwhile, J. J. Thomson discovered the electron; where did that come from? Becquerel discovered radioactivity; where did that come from? Röntgen discovered x-rays; where did those come from? It looked as if even as a new century was being ushered in, Nature was slowly raising the curtain on a whole new world of Physics! Some of that story we shall catch up with as we go along with our quest – by the way, that part of the story is very important to us!
Moving at the Speed of Light Let me now make the point I have been slowly inching towards all this while. You see, as the twentieth century began, Physics slowly began to cross two new frontiers. Frontier One was associated with very high velocities; what is meant by high? By high, I mean speeds approaching close to that of light. Remember, light travels roughly at 300,000 km per second, and just to give you an idea of what that means, let me tell you that it takes light eight minutes to reach us from the moment it leaves the Sun. If you think that is long, let me tell you that if a spacecraft close to say Neptune were to send an electronic signal now, it would take hours for that signal to reach us - this in spite of the signal travelling at the speed of light! Imagine having a telephone conversation with an astronaut on that spacecraft! You say hello, and that message takes several hours to reach him; he asks ‘how are you?’, and that takes more hours to reach the earth! To get back to what I was trying to say, we could make a diagram as below:
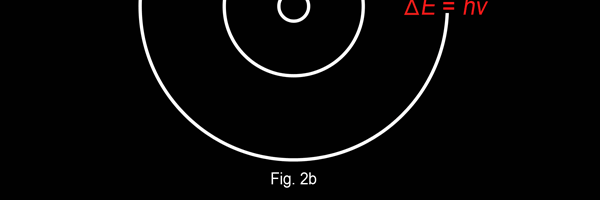
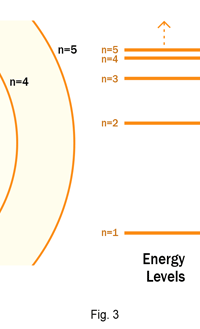
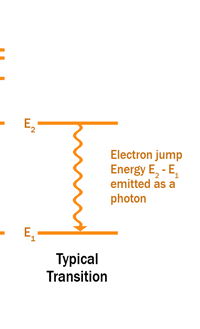
The above diagram is merely to put in perspective the developments that began regularly to shake Physics from about 1900 onwards; the story is not over, not by any means, and the most exciting chapter is yet to be written! Meanwhile, let us go back about a hundred years, when exciting events had just begun to happen. The year was 1912. Bohr tried a classical model for the hydrogen atom and failed. He knew something was wrong, but what was wrong and where? Where to put the finger to get at the solution? Bohr thought hard, and came up with a very original thought. Bohr said: “Let us go back to Planck’s explanation for the blackbody radiation spectrum. There are two interesting aspects to his analysis. First is that the energy of mechanical oscillators is quantised [see Fig. 8 in QFI 19]. Next, we must remember that according to Planck, radiation energy is itself quantised. These two facts seem to indicate that when we enter the world of the small, quantum effects apparently enter in some mysterious way and simply cannot be ignored. My classical model for the hydrogen atom failed to deliver because it totally ignored all quantum effects. Maybe, I should build in quantum effects in some manner or the other.” Starting thus, Bohr was able to tinker with his model and quickly come up with a brilliant improvisation. It was quite simple really, so simple that these days the Bohr model is taught even to high school students. So what was the great magic that Bohr performed? After a lot of thinking, Bohr argued, “When Planck tried to explain blackbody radiation, he assumed that the energy of the mechanical oscillators [remember the electrons on the walls of the cavity that were oscillating back and forth? See QFI 19] were quantised. This means that when one goes to very small distances, even mechanics begins to acquire some sort of quantum character. So why don’t I suppose that when an electron moves in an orbit around the nucleus, the angular momentum of the electron is quantised?” Atomic Equations For the benefit of those of you who do not know, I should mention that when an object of mass m moves with a velocity v, we say it has a liner momentum mv. Similarly, when an object of mass m moves in a circular orbit of radius r with a velocity v, then it has an angular momentum m v r. Now what Bohr was essentially saying was that the value of the quantity m v r could not be any arbitrary number but has to be one of a fixed set. What was that set? Here, Bohr made an inspired guess: “He said that Nature’s rule is that the angular momentum has to be an integer times the basic constant given to us by Planck, namely h.” Stated simply, Bohr’s rule was: Angular momentum = (nh) / 2π, where n is an integer and takes on values 1, 2, 3, …..etc. Now if you take this rule literally pulled out of a hat by Bohr, and remember that angular momentum is given by m v r, and further that m the mass of the electron is fixed, then clearly, only certain orbits would be allowed and not all the ones we might imagine to be possible. Thus, Bohr took a bold step and said: “Nature has ordained, that of all the orbits that might be possible in the classical picture, in reality only a set of preferred orbits [that obey the angular momentum quantisation rule] are allowed. The electron can move in these special orbits without the danger of spiralling down; these orbits are divinely ordained and therefore safe! These are stationary orbits, and what saves the electron from destruction when it moves in these orbits is the fact that they conform to the rule of quantisation of angular momentum [given above].” OK, all this is fine. But what about the light the atom emits? How does that come about in this picture? Bohr said that was no problem. And to understand Bohr’s explanation, take a look at Figure 2 below:
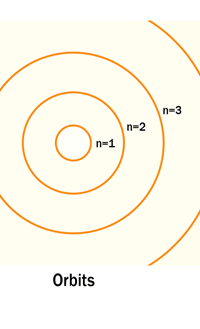
So you see, by introducing the idea of quantisation of angular momentum, Bohr neatly brought the atom into the fold of the quantum world. And from that, explaining line spectra was no sweat at all. First, take a look at the figure below.
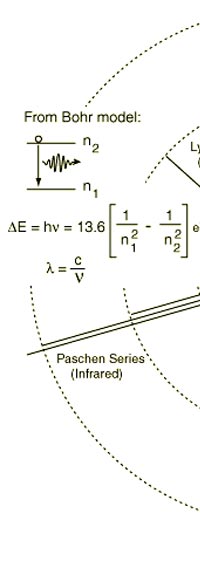
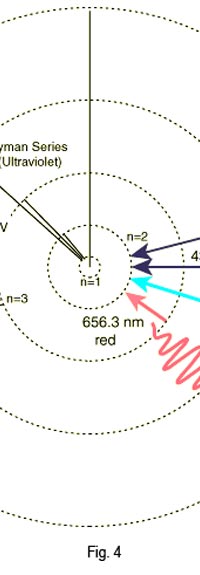
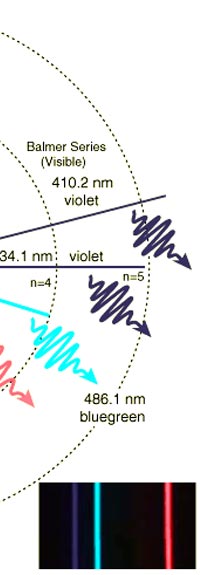
As they say, the proof of the pudding is in the eating of it. So how good was Bohr’s model of the hydrogen atom? It turned to be amazingly good! You see, physicists had already made a fairly detailed study of the spectrum of the hydrogen atom and found that the spectral lines could be divided neatly into various “families” known as the Balmer series, Lyman series, Paschen series etc., each series being named after the discoverer. Bohr showed that each series was the result of appropriate jump of the electron from higher energy levels to a particular lower energy level. Thus, as you would find from Figure 4.
Bohr’s model was unquestionably a great step forward. However, very soon, after all the cheering was over, people began to realise that Bohr’s model was just a model and not a theory. A theory is a regular grammar that lays down some basic rules which could then be applied to various situations. On the other hand, the model that Bohr gave was applicable only to the hydrogen atom. Indeed, as more careful experiments came to be done, it was found that it could not even explain everything about the spectrum of hydrogen, especially the finer details. Even worse, it was almost impossible to extend the model to the next simplest atom, namely helium, which had two electrons instead of one. If it was going to be so tough even for helium then what to say of more complex atoms like oxygen and so forth? All this did not mean that people began to dismiss Bohr’s work. On the other hand, they realised that it was trying to give a coded message. Part of the message was clear, which was that if one wanted to understand atoms, then one had better be ready to apply quantum ideas. But how exactly was this to be done? No one knew, indeed for nearly fifteen years. After that incubation period when ideas were being cooked, the answers came, and they were of a quite surprising nature; indeed, they did not come because people were looking at more complex models for the atom. Rather, they came because physicists were now looking for an honest to goodness quantum theory. That story is reserved for the next issue! (to be continued...)
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Vol 6 Issue 11 - NOVEMBER 2008
|
Best viewed in Internet Explorer - 1024 x 768 resolution. |