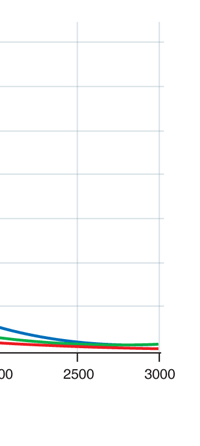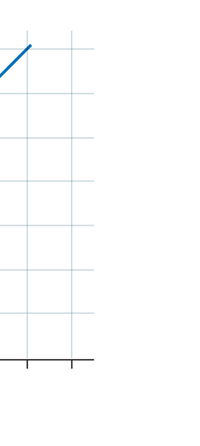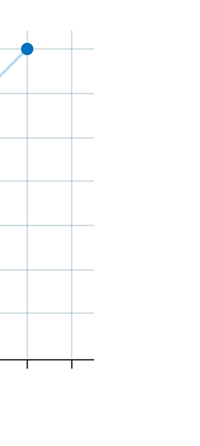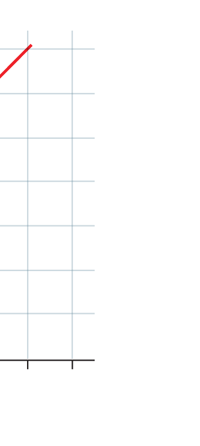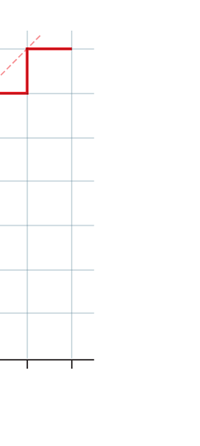|
 |
 |
Volume
6 - Issue 09
SEPTEMBER - 2008 |
By Prof. G. Venkataraman
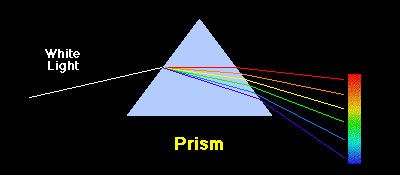
Loving Sai Ram and greetings from Prashanti Nilayam. In the last issue, I gave you a glimpse of the evolution of Classical Mechanics and how when it came to modelling the atom using the solar system as a guide, Classical Mechanics seemed to give way. This is a major turning point in the history of Physics, and was one of the many precursors to the birth of what is called Quantum Mechanics. Very soon, we are going to delve into some of the mysteries of Quantum Mechanics because it would take us to the very door-step of Meta Physics. It is therefore useful to spend some time recalling a few bits of early history, so that we get a better idea of how many pieces of the jig-saw puzzle popped and how in a remarkable way, the pieces began to slowly fit together to reveal an amazing tapestry that underlies Creation. The Sun’s Medley of Colours I would like to begin with what are called atomic spectra. The story of atomic spectra is intimately connected with the work of Niels Bohr that I started to describe in the last issue, and unless we get to know something about atomic spectra, it would not be possible to understand why Bohr was trying to come up with a model for the atom. To being at the beginning, I must really go back to Newton, who clearly demonstrated that what we regard as while light coming from the Sun is actually a medley of colours – this was sort of known for a long time thanks to the rainbow – but Newton it was who confirmed it by first splitting the white light of the Sun into seven colours of the rainbow, and then recombining the colours to get back white light. What it all showed was that sunlight consisted of a broad spectrum of colours.
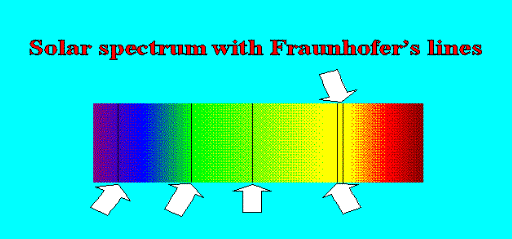
Darkness within Light In 1802, Wollaston tinkered with the slit a bit by way of improving the instrument resolution and he discovered that the spectrum of sunlight had some dark lines. In 1814, Fraunhofer used improved techniques and discovered that the spectrum had plenty of dark lines, hundreds of them. He had no idea of why these lines were present, but having discovered something new, his name automatically got attached to these lines – they are called Fraunhofer lines see Figure 2.
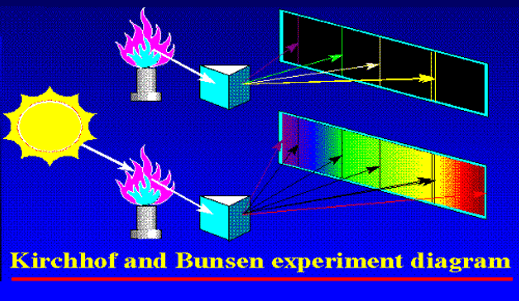
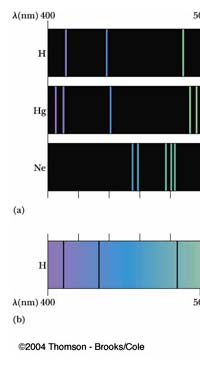
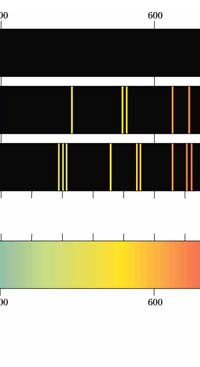
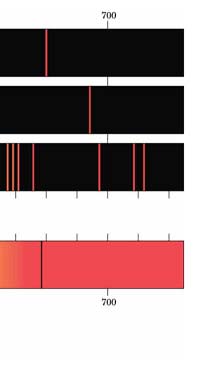
In 1851, Masson did the experiment shown in Figure 3. What he found was that sparks created with rods of metals, when examined with a spectroscope revealed sharp lines. These lines were of different colours and they began to be called spectral lines. Masson further found that different rods made of different metals yielded different sets of lines. People learnt to photograph these line spectra and such spectra became a way of finger printing different metals. Indeed, this was the beginning of what has come to be called emission spectroscopy.
In 1859, Kirchoff and Bunsen demonstrated that while metals when made hot emit spectral lines, something interesting happens when light from a continuous, broad-spectrum source is made to pass through a metallic vapour that is cold. When the light emerging from the vapour is examined with a spectroscope dark lines appear precisely at those frequencies where bright lines appear in emission spectra. Thus, absorption and emission of light by different substances are complementary phenomena. Everyone knew that different atoms had different characteristic spectra and in fact atoms could be finger-printed [these days people talk of DNA finger-printing; spectroscopic finger-printing of atoms started much earlier]. See also Figure 3.
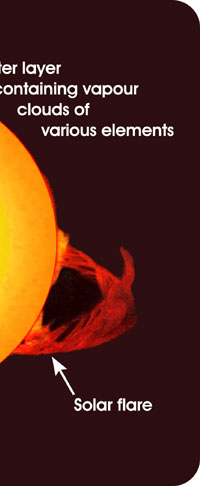
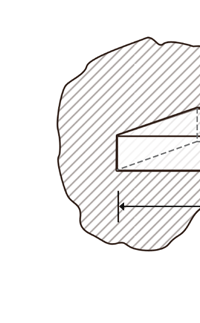
Once Kirchoff and Bunsen understood all about this complimentarity that I just mentioned, it was simple for them to explain the Fraunhofer lines; the dark lines in the spectrum of sunlight were due to absorption by different kinds of atoms in the Sun. Now where exactly were these atoms? Kirchoff and Bunsen had an answer for that also – see Figure 5. They said that while the interior of the Sun was very hot, the outer layer was relatively cool and had vapours of many elements. The light coming from the interior of the Sun was a continuous spectrum, and when that light passed through the outer layers, atoms of different species grabbed bits and pieces of light to cause dark lines. Given the fact that these two had already demonstrated the principle of complimentarity between emission and absorption, this explanation for the Fruanhofer lines seemed acceptable.
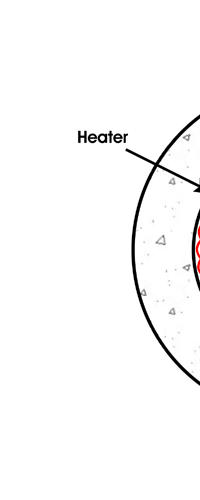
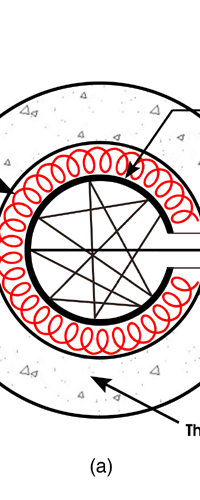
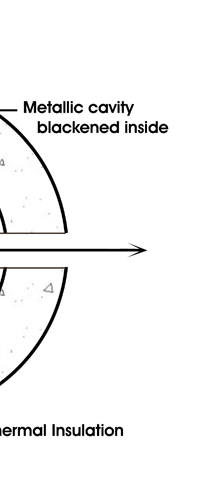
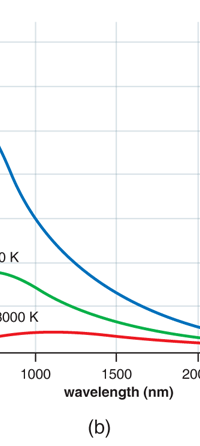
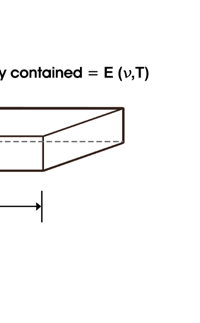
In 1859, Angstrom in Sweden who had been observing the solar spectrum for years, published a detailed compilation of all the dark lines he could catch in his years of painstaking study. Black-Body Radiation We now move to the year 1900, when the new century was heralded with a major discovery by Max Planck of Germany. That story goes as follows, and before I tell you what happened in 1900, I must give you some background. Let me start with what is called a black body. In physics, a black body is an object that absorbs all light that falls on it. No electromagnetic radiation passes through it and none is reflected. Because no light is reflected or transmitted, the object appears black when it is cold. If the black body is hot, these properties make it an ideal source of thermal radiation. If a perfect black body at a certain temperature is surrounded by other objects in thermal equilibrium at the same temperature, it will on average emit exactly as much as it absorbs, at every wavelength. Since the absorption is easy to understand—every ray that hits the body is absorbed—the emission is just as easy to understand. The term "black body" was introduced by Kirchoff in 1860. The light emitted by a black body is called black-body radiation. At this stage, I would like you to take a look at Figure 6, which would give you some details about a black body and the radiation it emits.
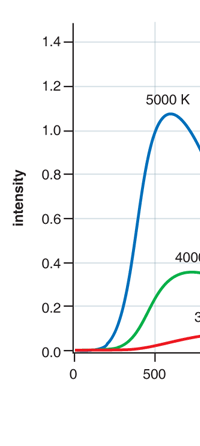
If a small window is opened into an oven, any light that enters the window has a very low probability of leaving without being absorbed. Conversely, the hole acts as a nearly ideal black-body radiator. This makes peepholes into furnaces good sources of blackbody radiation, and some people call it cavity radiation for this reason. As the temperature decreases, the peak of the black-body radiation curve moves to lower intensities and longer wavelengths. The black-body radiation graph is also compared with the classical model of Rayleigh and Jeans.
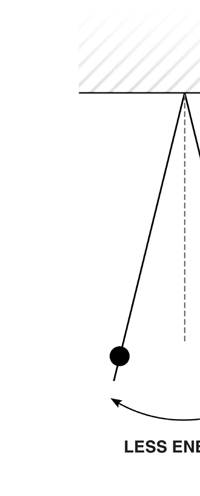
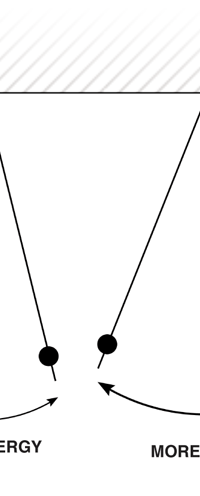
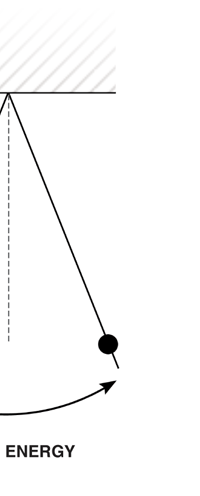
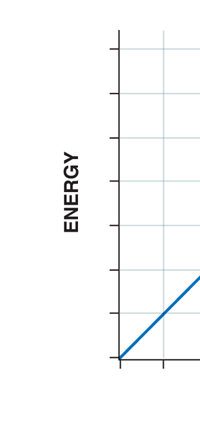
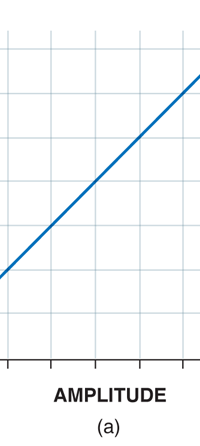
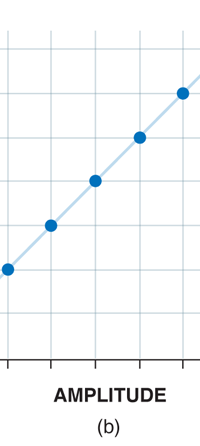
I would now like to pick up from the quantity E(ν, T) introduced in Fig. 6. Kirchoff noted that the shape of the curve E(ν, T) would depend on the absolute temperature T of the black body and challenged experimentalists to measure it accurately; he also challenged theorists to explain the form determined by experiments. So that became the game for many decades preceding the dawn of the 20th century. What happened was that from the side of the theorists, there were two formulae that worked but only for a limited region. One was called the Rayleigh-Jeans formula and that worked at the low frequency end. There was another formula called Wien’s law that appeared to work at the high-frequency end. All this was patch work; obviously what was needed was one formula that worked all the way, that is, for the entire spectrum. Planck’s Brainwave In October 1900, the German scientist Rubens who was then doing experiments on black body radiation, paid a visit to Planck. Rubens was accompanied by his wife and it was a social call. But during the conversation Rubens told Planck that his latest data did not agree with Wien’s formula, which was therefore suspect. Planck then began to think about the problem; at that time, he was not aware of the work of Lord Rayleigh. By the next day, Planck invented a formula, which seemed to agree with the result of Rubens. Planck then scribbled the formula on a post card and mailed it to Rubens. The formula was not derived, but simply pulled out of a hat by sheer intuition but it was an amazing guess. In the formula, Planck had a constant, for which we now use the symbol h; in honour of Planck, it is now called the Planck’s constant. All this happened in October 1900. Planck’s formula worked very well but Planck was not satisfied with that. Was his formula a mere fluke or did Nature have something behind it? Planck thought about it deeply for a couple of months, Planck was actually able to derive the formula; it was no longer magic but based on a model or theory, shall I say? The way Planck argued is summarised in BOX 1, and so I shall not go through it here. But I do have to make a reference to the implications of his theory because the implications were profound. To appreciate the importance of the discovery that Planck made, let us first consider a simple pendulum, as illustrated in Figure 7. I am sure you would agree that we could, in principle make the pendulum oscillate with different amplitudes, simply by pulling it from equilibrium to different distances and letting it go. I am sure you would also agree that the larger the amplitude of oscillation, the greater would be energy of pendulum.
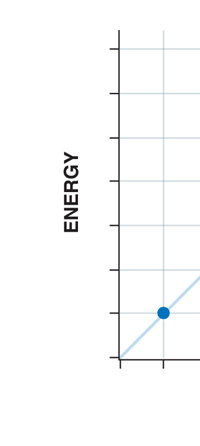
If now I were to make a graph of energy of the pendulum versus the amplitude, it is reasonable to expect it to go as in Fig. 8a. What Planck discovered was [to his amazement of course], that when very low energies are involved, the energy of an oscillator [for that is really what the pendulum represents] cannot be increased continuously but only in a step-wise fashion as in Fig. 8b, that is to say, energy can be increased only in fixed quanta. This led to the view that the energy of light is bundled in quanta, something that no had ever suspected till then.
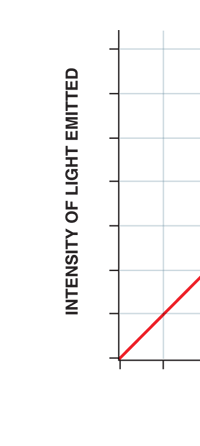
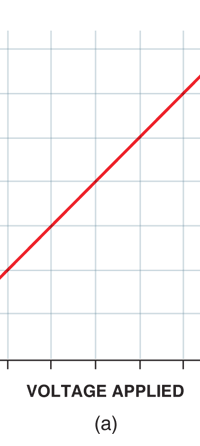
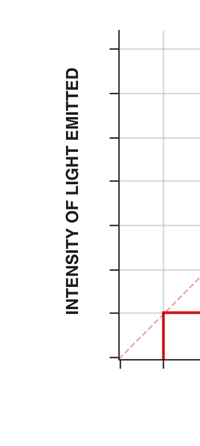
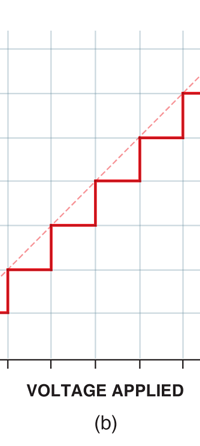
Now this implication of Planck’s discovery made everyone rather uncomfortable. Why? That is what I shall try to explain next. You see, when we have a light source that emits light, that source is actually emitting energy; and this energy is carried by the light waves – by the way, for nearly two hundred years, physicists firmly believed that light consisted of waves, that is to say when a source emits light, the energy radiated is carried in the form of waves. This is true whether the source of light is an ordinary electric bulb or the Sun itself – that is point number one. Point number two was that this energy is continuous. Now what do I mean by that? Suppose we have a light source that emits at just one frequency; such a light source would be called a monochromatic source and these days it is possible to have such a source [almost!]. So we have this source and use a control know to slowly make this source emit more and more light; this control, by the way, is assumed to be extremely sensitive and capable of being operated in such a manner that the light intensity is increased truly by infinitesimal amounts – all this is hypothetical of course, but that does not matter. The point is that if there is such a source and we did increase the intensity gradually [say by increasing the voltage], then the graph of voltage versus intensity we would expect would be as in Fig 9b; this is what we would expect from the wave theory of light, which is what everyone believed in, and which was also sanctified by Maxwell [remember his name from the last issue?]. OK, all this is fine, but what has all this to do with Planck and his discovery? That is what I am coming to now. Planck found, much to his discomfort I should say, that radiation energy is actually bundled; he was forced to this conclusion by his attempt to explain the character of black body radiation. In this picture, the graph that you saw in Fig 9b changes to that in Fig 9c; the curve does not increase smoothly but in steps. Not very comfortable, thanks to at least a century [if not more] of firm belief in the wave theory of light, given the ultimate seal of approval by Maxwell himself. It looked that Nature was not all that simple but hiding a lot of secrets that she was not yet ready to reveal fully!
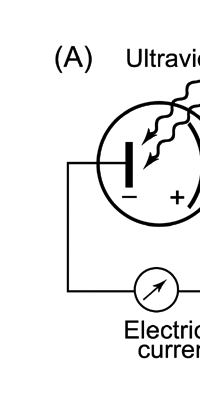
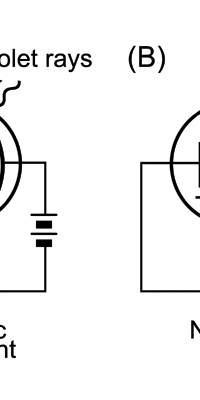
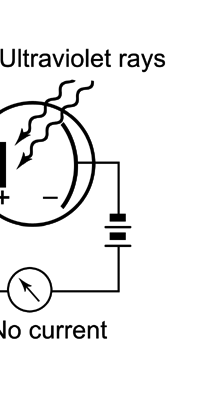
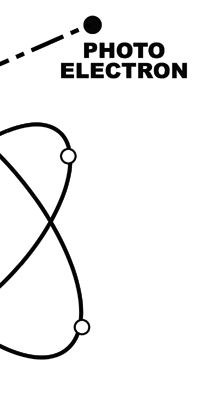
Einstein Makes Another Historic Discovery As always, one thing leads to another, and the next step was taken by Einstein. The year was 1905, during which, Einstein, who was then a clerk in the Swiss Patents Office [did you know that!] working in his spare time [those were days when the boss did not chase his minions all the time with cell phones, blackberrys and all that!], wrote three amazing papers, each worth a Nobel Prize; however, he ended up getting only one, and that too only as late as 1922! [But much before that he had become world famous, achieving what we would now call rock-star status.] So what was the great thing that Einstein did that shed some light on the puzzling discovery of Planck? That story next. The story that I just referred to has to do with what is called photo-electric effect. Basically what it means is that when light falls on a metallic plate, electrons are emitted. The phenomenon was discovered by Hertz of Germany, while it was his student Lenard who established that the electrically charged particles emitted when light falls on a metallic plate are actually electrons. Figure 10 below explains what the effect is all about.
There is more to the story, and that is really what it makes it both interesting and important as well. To take the story further, we go back in time to the year 1905, and find out what Einstein was doing then. I already told you that it was in that year that Einstein made three monumental discoveries, and one of them was his explanation for the photo-electric effect. By the way, remembering the amazing contribution that Einstein made way back in 1905, the year 2005, was declared to be and celebrated throughout the world as the Year of Physics. Now what was the big deal about Einstein’s work on photo-electricity? Well, prior to Einstein’s work, it had been found that emission of photo-electrons had the following properties:
These observations baffled physicists for many decades because they all tired to explain the experimental observations on the basis that light energy existed and propagated as waves. This was a perfectly normal thing to do in those days because everyone firmly believed that light existed as waves and that that was all there was to it. Now, if light were to be a wave, both the energy and the number of the electrons emitted from the metal should increase with an increase in the intensity of light. Observations contradicted this prediction; only the number, and not the energy, of the electrons increased with the increase of the intensity of the light. Why was this so? No one could give the answer, and that was where Einstein stepped in. Einstein was aware of the recent work of Planck and he said to himself: “Everybody says that light exists as waves but the wave theory could not explain the spectrum of black body radiation. This guy Planck says he can explain the spectrum, provided one assumes the light energy comes bundled. If there is light of some particular frequency v say, energy associated with that frequency is available in Nature only in packets containing hν, 2 hν, 3 hν, …… of energy. Making this assumption, Planck managed to explain the black body radiation spectrum. Now in the case of the photo-electric effect, the wave theory of light seems to be going nowhere. So why don’t I give this fellow Planck’s idea a try and see where it takes us?” Essentially that is how Einstein got started, and lo and behold, he literally hit the jackpot, meaning that he actually succeeded in explaining the till-then-mysterious photo-electric effect.
Einstein basic idea is illustrated in Figure 11 above. He said first let us assume that light energy comes bundled in quanta, the way Planck says they would. Now when a light quantum hits an atom, it knocks out an electron. Now in the actual experiments, they allow light to fall on a metallic plate. The electron emitted may not quite be able to fly away from the plate and might be held by the plate; this was known from earlier experiments, and a physicist named Richardson had actually determined the minimum energy an electron at the surface would need in order to escape for various metals. This minimum energy was called the work function of the metal and was denoted by the symbol W. Keeping this in mind, Einstein argued That if a light quantum of energy hv kicked out an electron from the atom, the plate would grab its share W and therefore the maximum kinetic energy the electron could have when it came out of the plate would be E = hv – W. In 1916, Millikan in America did a series of very thorough experiments and he not only proved that all the implications of Einstein’s theory were correct but was also able to determine the value of the universal constant h introduced by Planck [which, I told you earlier, is now called the Planck’s constant]. In spite of all this, there was a lot of reluctance to accept the idea that light energy actually was bundled up in quanta, and it was not until 1922 that the Nobel Committed in Stockholm finally decided that they had to honour Einstein [who in the meantime had already become a great celebrity] with the Nobel Prize. Actually there was a problem for which discovery they should honour Einstein, and the wise men of Stockholm decided it would be for his explanation of the photo-electric effect. Those were the days when they did not have jet planes; in fact, even air travel, especially over long distances was simply unthinkable. The Nobel Prize announcements were made towards late October I believe, and by that time, Einstein, on account of prior commitments, was on a long tour to Japan and many other places. Thus, on the day when the prizes were actually handed out, he could not be physically present in Stockholm actually to receive the Prize from the King of Sweden; but then, as many said, it was the Prize that was honoured rather than Einstein himself! Atomic Quantities It is time to come back to a question that I left you with in the last issue, namely Bohr and his attempt to construct a model of the atom. If you recall, the year was around 1910/1911 or so, and Bohr was trying to construct a model of the atom, that included a tiny nucleus that carried all the positive charge in the atom, and equally tiny electrons whirling around this nucleus, rather in the manner planets move around the Sun. OK, but why would Bohr want to do all that? What was the immediate objective, if any? The first and foremost point is that atomic spectra seemed to consist mainly of lines bundled together. See figure 12.
The question was why do atoms emit line spectra? Further, could one explain the spectrum of different elements by making some model of the atom? That was what Niels Bohr was really after. As we saw last time, he started by imagining that atoms were tiny, tiny replicas of the solar system and applied classical mechanics but that got him nowhere. Bohr now began to do some serious thinking. He told himself, “Looks like for some reason classical mechanics is not working. Could this in any way have anything to do with the fact that light energy is bundled in quanta? After all, that is what Planck said and Einstein has gone further and argued that unless one takes the idea of light energy being bundled in quanta, one simply could not explain the photo-electric effect. Maybe, since I am dealing with light emitted by atoms, I too have to somehow work in the idea of quantisation into my model of the atom." By rather clever ideas, Bohr actually managed to pull it off. That story next time! Hope you are liking this narrative. By the way, these days even high-school students learn about the Bohr model of the atom. But that does not reduce its revolutionary nature and the tremendous impact it made on physics at the time of its discovery. In fact, it was something like a turning point. What happened was the Bohr atom suddenly gave a clue to why atomic spectra were organised in lines; not only that; Bohr was completely able to explain the spectrum of hydrogen, the simplest of elements. However, when his model was applied to helium, the next simplest element, there was trouble galore. So once again the some story – part of the truth no doubt but something is missing. And so step by step, chasing one missing link after another, physicists were led to Quantum Mechanics – that happened roughly during the years 1925-1930. That was the major turning point that I am slowly taking you to. You know what? So spectacular were these developments that some people – that included even some big shots – said physics was over and the rest was all chemistry. How wrong they were! All that comes later. And don’t worry, hidden in all this mystery is the INFINITY that we are after. I have not forgotten that goal even if you might have! See you again next month; meanwhile, take care! Jai Sai Ram.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Vol 6 Issue 09 - SEPTEMBER 2008
|
Best viewed in Internet Explorer - 1024 x 768 resolution. |