|
 |
 |
Volume
6 - Issue 12
DECEMBER - 2008 |
By Prof. G. Venkataraman
Loving Sai Ram and greetings from Prashanti Nilayam. I do hope you recall where we left off last time. Basically I told you that via his model for the hydrogen atom, Niels Bohr, managed to get a toe-hold into a new world.
But little did he know at that time, how revolutionary and incredible this new world was and how it was going to dominate not only Physics but indeed most of Science and even day to day life in an incredible fashion for the rest of the next century and indeed into the 21st century as well! In this instalment, we shall try and get a glimpse how the first few chapters of that story unfolded in the two decades or so following Bohr’s triumph. As I told you last time, Bohr’s model was very tantalising; it seemed to explain very nicely many previously known facts about the hydrogen spectrum that were totally baffling. However, the model was of no use at all one step beyond hydrogen, that is to say, where the helium atom was concerned, it fell totally flat. In fact, it was soon discovered that even where hydrogen was concerned, there were many subtleties that the Bohr model failed to explain. From all this it was clear that what the Bohr model had really succeeded in calling attention to was that if progress was to be made in the world of the small, then some radical quantum ideas were needed. What exactly were those ideas? De Broglie Visualises the Duality of Matter People began furiously searching all over the place and the first clue about how to change one’s thinking came from Prince Louis de Broglie of France. De Broglie put forth a simple idea. He said, “Listen we now know that where light is concerned, it has two aspects, a wave aspect known to us for over a century and a quantum aspect first suspected by Planck and later made much clearer by Einstein. Now I wonder whether matter too has a dual aspect. We all know it has a particle aspect, but could it be that it has a wave aspect too that becomes important when one goes to small distances like in an atom?” Was de Broglie just tossing a wild idea or did he have some basis for thinking so? It turns out that he did have a hunch, and argued as follows: In the case of light, we know three things:
De Broglie now boldly suggested: “I say that if there is a particle of mass m that is moving with a velocity v [so that its momentum is mv], then there is associated with this particle a wave whose wavelength λ is given by λ = (h/mv).” Now this was a daring conjecture, and De Broglie made this suggestion in 1923. Soon this prediction was proven to be correct by two independent experiments, one done by Davisson in America and the other by G.P. Thomson in England. Working with electron beams, they showed that these beams got diffracted as if they had a wave aspect. See Fig. 1
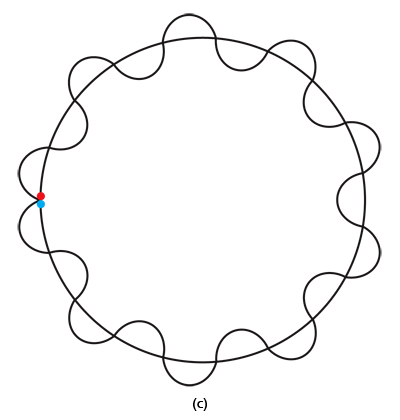
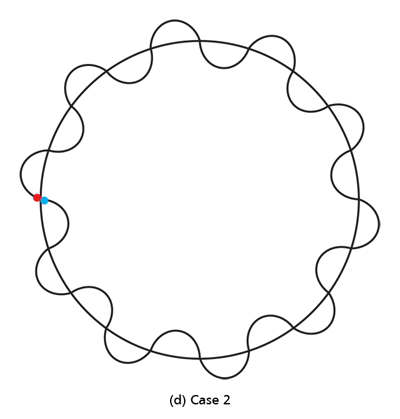
By the way, it is interesting that G.P. Thomson was the son of J.J. Thomson who discovered the electron. If you recall, JJ identified the electron as a particle and also measured its mass. The son demonstrated that the electron also behaved like a wave! All in the family – happens sometimes! Wrapping Up Electrons’ Orbits To get back to the main story, people now began to say, “We think we can understand why Bohr speculated that not all orbits are allowed for the electrons and why only some are allowed.” Their argument went something like this. Take a particular orbit. For the electron to move in that orbit, whose radius is say r, it must have a particular velocity v say. If the mass of the electron is m, then the momentum in that orbit would be mv. One can now use de Broglie’s formula and calculate the associated wavelength λ. Now draw a circle of radius r, and try to wrap a wave of wavelength λ around this circle. There are only two possibilities; either one can wrap an integral number of wavelengths around the circle or one cannot – see figure below.
If one cannot wrap an integral number of wavelengths, then it means that nature does not favour that orbit; on the other hand, if one could do such a wrap, then that is a preferred orbit. In this way, some justification was found for why Niels Bohr was forced to choose some orbits and reject others – it all seemed to be connected with the wave aspect of the electron. However, all this was just hand-waving; what was needed was a proper theory. And that came as the result of independent efforts by three different people in three different countries! That story next. This is not exactly a historical account of how it all happened, but roughly speaking, the three pieces of the story referred to above can be described as follows. First there was Schroedinger in Austria who said, “If according to de Broglie matter has a wave aspect of it, let me introduce a quantity Ψ [Greek symbol, pronounced 'psi' ] which I shall call a wave function. This wave function should describe for me the wave-like behaviour of matter.
For example, if I want to know about what the electron in a hydrogen atom does, I shall start with the idea that Ψ represents the wave function of the electron in the hydrogen atom. This Ψ should depend on where the electron is and so I shall make that explicit by writing the Ψ as Ψ(x, y, z). This way of writing enables me to describe the wave function at every point with co-ordinate (x, y, z). Now how do I find this mysterious Ψ? Well, let me now write down an equation that this wave function would satisfy, in this case an equation specific to the hydrogen atom.” Schroedinger figured out a way of writing such an equation and this equation is now called the Schroedinger equation. So the first thing one must do if one wants to solve a problem is to write the Schroedinger equation for that problem. This equation happens to be what is called a differential equation, and differential equations are quite familiar in mathematics. So, having written down the equation, one now goes about solving the equation, and when one does that, one gets many solutions. In the case of the hydrogen atom, it turns out that these solutions represent the different ways in which the electron can behave in the hydrogen atom. As one expected, these different solutions did have some connection with the intuitive picture that Bohr had conjured up earlier. However, from Schroedinger’s more detailed and scientifically superior analysis, it emerged that the idea of orbits is meaningless! We shall come to that later. One strange thing that happened was that in general this wave function Ψ could be a complex quantity instead of a real quantity. I am sure that would fox many of you and so at this point I must make a few introductory remarks about real, imaginary and complex numbers. The Meaning of Imaginary Numbers Real numbers are what we deal with normally. Whole numbers could be integers like 1, 2, 3, …etc., fractional numbers like 3.14, 17. 832 etc., and negative numbers like – 24, - 6.5 and so on. All these are examples of real numbers and we understand what they mean. Now consider square roots; I am sure everyone knows that the square root of 4 is 2, the square root of 25 is 5, and so on. Similarly, the square root of 1 is just 1; I am sure you know that also. Now suppose I ask: What is the square root of the negative number – 1? This is a perfectly valid question to ask. It turns out that, as all of us know, that there is no real number that can qualify to be the square root of – 1. Does that mean that the square root of -1 does not exist? Mathematicians say, “Of course it does; however, that square root is an imaginary number!” Now you and I may not be comfortable with imaginary numbers but in mathematics not only are they freely allowed but also found to be very useful. The square root of -1 is denoted i. What it means that i x i = -1. I am not too sure that makes things a bit clearer, but even if it does not, please just accept that the imaginary number i introduces a new set of numbers called complex numbers. That is what I shall explain next. Now once one allows room for the imaginary quantity i, then one can straight away introduce complex numbers like (3 + i4). One says that this complex number has two parts, a real part with a value 3, and an imaginary part with a value 4. I am mentioning all this because it was found that in general, the wave function that Schroedinger introduced was a complex quantity, that is to say, it had a real as well as an imaginary part. What sort of a meaning was to make of this complex matter wave? That remained a problem till Max Born showed a way out; I shall come to that later. The ‘Incredible Simplicity’ Discovered by Heisenberg Let me now turn to another very different chapter in the evolution of quantum mechanics. This chapter was written by young Werner Heisenberg, quite independent of Schroedinger. Heisenberg was 24 when he did the work that got him an entry into the Hall of Fame of Physics. At that time, having finished his doctorate, Heisenberg was spending time in Copenhagen in Bohr’s Institute, having won a Rockefeller Fellowship. One day, he suffered an attack of hay fever and was advised to withdraw to an island called Helgoland where grass did not grow. Here, Heisenberg was literally all alone. With hardly anything to do and plenty of time to think, Heisenberg began playing round with an old problem he had become interested in as far back as 1922. He decided to attack the problem in an unusual way, inspired by recent developments that strongly suggested that Nature had a quantum aspect. One evening, he caught on to a new way of looking at the problem but was making many arithmetical errors because the calculations were long and tedious. However, he pressed on and it was quite late when he could finish it. This is how he recalled it later: “It was almost three o’clock in the morning before the final results of my calculations lay before me…. And I could no longer doubt the mathematical consistency and coherence of the kind of quantum mechanics to which my calculations pointed. At first, I was deeply alarmed. I had the feeling that, through the surface of atomic phenomena, I was looking at a strangely beautiful interior, and felt almost giddy at the thought that I now had to probe this wealth of mathematical structure Nature had so generously spread out before me. I was far too excited to sleep.” To his wife he wrote later: “I was lucky to look over the good Lord’s shoulder while He was at work.” And to his sister he said, recalling those exciting moment of discovery: “… the last few weeks were full of excitement for me. And perhaps I can best illustrate what I have experienced through the analogy that I have attempted an, as yet unknown, ascent to the fundamental peak of atomic theory….. And now, with the peak directly ahead of me, the whole terrain of interrelationships in atomic theory is suddenly and clearly spread out before my eyes. That these interrelationships display, in all their mathematical abstraction, an incredible simplicity, is a gift we can accept only humbly. Not even Plato could have believed them to be so beautiful. For these interrelationships cannot be invented; they have been there since the creation of the world.” Heisenberg’s Uncertainty Principle Heisenberg also made one more monumental discovery, central to the quantum world, namely the famous Uncertainty Principle. In the popular world, this principle is often misquoted and stretched beyond its legitimate limits, but historically, what happened was the following. Heisenberg began his paper by observing that his objective was “to establish a basis for theoretical quantum mechanics founded exclusively upon relationships between quantities which in principle are observable.” Thus it is that not only did observables become an important element of Quantum Mechanics but, along with it [though a bit later], the notion of the OBSERVER! After all, if a thing has to be observed, there has to be an observer, is it not? Those are philosophical matters to which maybe we shall come later, but the point I want make is that Heisenberg said that he wanted to establish a quantum rule book that would spell out the grammar for making calculations relating to quantities that could be observed in an experiment.
Now two of the most fundamental entities that one assumes to be observables in classical mechanics are the position and the velocity of a moving particle. That is to say, one asserts, that at every specific instant of time, one can determine where exactly the particle is; and, in principle, one could simultaneously measure the position and the momentum of the particle to infinite accuracy. Let us rephrase this remark to see what exactly it means. It means that in Classical Mechanics, one can in principle, know both the position and the momentum of a particle simultaneously, and with infinite accuracy – in practice this might be a tall order but there is nothing in principle that forbids this; that is what the rule book says in Classical Mechanics. Please note that when we draw trajectories for bullets and the like and actually calculate these trajectories using Classical Mechanics, we are actually assuming implicitly that we can know with infinite accuracy at every instant, both the position as well as the momentum of the particle. Until the advent of quantum mechanics, no one had any reason to suppose that this was theoretically impossible; yes in practice there might be some errors, but in principle, there was no conceptual obstacle. Heisenberg decided to see if this rule applied in the new quantum world also and to his surprise and astonishment he discovered that it did not always do so. He found, for example, that the position and momentum of a particle could never, even in principle, be determined simultaneously with infinite precision. If the position is measured with very high accuracy, then that very act of measurement would disturb the particle to change its momentum. Likewise, if the momentum is measured accurately at a particular instant, then that would upset the position and so the measurement of the position would give inaccurate results. For some strange reason, Nature seemed to have paired off certain observables in such a manner that they could never even in principle, be simultaneously measured with infinite accuracy. Heisenberg went further and determined a rule that goes as follows: Let Δp be the uncertainty in the measurement of the momentum p of a particle at a particular instant. Similarly, let Δx be the uncertainty or error in the measurement of the position x of the particle at the same instant. The point here is that uncertainties in measurement are unavoidable. And so an observer, despite all the care he takes, has these uncertainties in his simultaneous measurement of the momentum and position of a particle. Heisenberg then went on to show that these two quantities are related by the formula: Δp Δx > or = (h/2π), where h is Planck’s constant and the symbol > means greater than. In other words, there is always a minimum error, reflecting a certain basic uncertainty in Nature when we try to simultaneously measure two quantities that seem to be tied up peculiarly. This is a feature totally absent in Classical Mechanics. Dirac Creates the Quantum Mechanics Framework
Schoredinger and Heisenberg were like two people, feeling two parts of an elephant. The man who tied it all up and said that what these people were feeling was really part of one piece called Quantum Mechanics was Dirac, who came into this game in a strange manner. Let us hear that story from Dirac himself: “The first I heard about Heisenberg’s new ideas was in early September 1925, when R. H. Folwer [Dirac’s thesis adviser] gave me the proof sheets of Heisenbeg’s paper. At first I could not make much out of it, but after two weeks I saw that it provided the key to the problem of quantum mechanics. I proceeded to work it out for myself.” Later, Dirac said, “At that time, I was expecting some kind of a connection between new mechanics and the Hamiltonian dynamics [this is a reference to the complete edifice for Classical Mechanics that had been built up earlier in the 19th century by Hamilton]. I felt that when the quantum numbers became large, quantum systems tend to behave rather like classical systems.” So that puts Dirac’s work in some perspective. Basically, Schoredinger said, “If matter has a wave like behaviour, let me write down an equation for matter wave and examine what they predict.” This analysis led to what are called wave functions, associated with various states of the system. Around the same time, quite independently, young Heisenberg made some basic discoveries. They are:
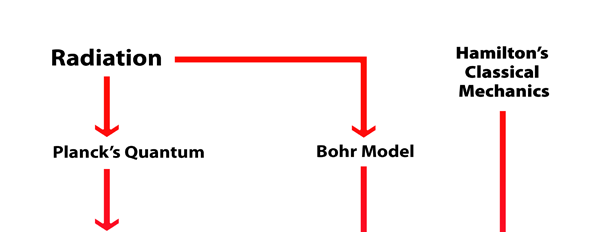
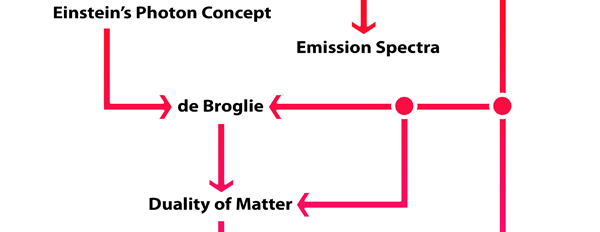
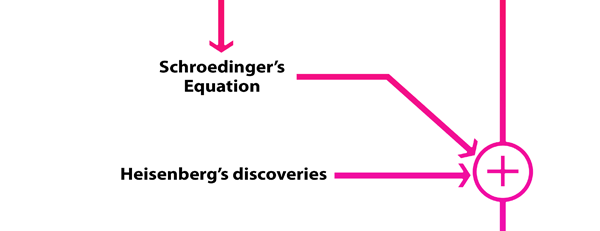
What Dirac did was to put all this together into a nice and most elegant framework, so that one had a complete working scheme for making practical calculations for a quantum system, just as Hamilton had given a complete scheme for a classical system almost a century earlier. In a manner of speaking, Dirac followed the same route as classical physicists normally did, but built into it all the quantum exceptions. Dirac initially published his work as papers but finally wrote a book, which became a classic. For generations, this was like the Bible, and so many learnt their quantum mechanics from this book. With good justification, it was often hailed as the book of the century! Figure 3 offers a rough flow diagram of how the various ideas evolved.
Dirac’s beautiful consolidation and “synthesis” of the different ideas literally gave one a rule book for doing practical calculations using the tools of quantum mechanics [of course ignoring relativistic effects, which one could afford to on many occasions]. Thus it is that Dirac at one time during that period went to the extent of saying that Physics was almost over and the “rest is all chemistry”! That of course was a fatally flawed prediction! But the fact is that like Hamilton’s tool box for Classical Mechanics, thanks to Dirac there was now a Quantum tool box, which was a must at the atomic and molecular level. However, the story does not end there; in fact it begins there! The first big question was: “What on earth does the wave function of Schroedinger represent? Does it have any physical meaning?” The question was a legitimate one, because Schroedinger’s Ψ was a complex quantity. How could a quantity with an imaginary part have any meaning in Physics, which dealt with physical reality? Yet, this Ψ delivered answers; so clearly, there was something to it. But how does one make any meaning of it? The answer to that question was first attempted by Max Born, and that was a real breakthrough. But it also opened the Pandora’s box, and some of the problems raised over seventy years ago, are still with us! All that story later. (to be continued...)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Vol 6 Issue 12 - DECEMBER 2008
|
Best viewed in Internet Explorer - 1024 x 768 resolution. |
DHTML Menu by Milonic |